续前:
2、《讲义》第21页 见图2.12,图中:P=15.35 KN
2R=2RA=2×29.7=59.4 KN (原“讲义”中有误)
q =5.26 KN/m
Mmax=(1/2) q×1.22+(p+2RA) ×1.2=3.8+89.7=93.5(KN.m)
Vmax=2×29.7+15.35+5.26×1.2=81.1
D=M/fcbh20 =81.1×106/14.3×250×6652 =0.059
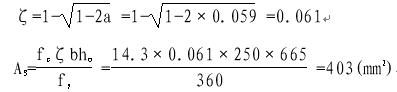
实际选用3Φ25 As=1471>403
满足要求.
V=59.5×103<0.25Bcfcbho=0.25×1.0×14.3×250×665=594×103
[该公式为判断验算条件的公式见《混凝土结构设计规范》(7.5.1-1)]
该梁的实际抗剪能力为(见《混凝土结构设计规范》(7.5.4-2))
VS=0.7ftbho+1.25fw(ASV/S) ho
=0.7×1.43×250×665+(1.25×360×78×665)/100
=166416+234911=401327(N)>93500
满足要求
3、续前《讲义》22页
LL2梁计算:该梁为多跨连续梁,本文按三跨连续梁计算,为减少繁琐计算本文也未按活荷载的最不利分布进行计算,计算简图如下:
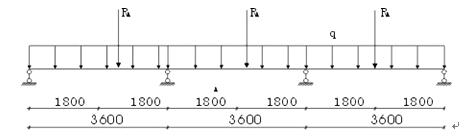
本来在支座处亦有RA作用,但对求连续梁内力不起作用。
LL-2与走廊现浇板同时浇筑,我们可按“7”型梁计算,其截面如下图所示:

荷载计算:梁自重(均布)q=25×(0.5×0.2+0.1×0.55) ×1.2
=4.7(KN/m)
RA=槽钢挑梁传来支座压力=29.7(KN)
内力计算:LL-2已为连续梁(超静定结构),按三跨三续梁计算,因RA计算时与脚手架立杆压力有关,而计算立杆压力时考虑了架体上同时有二层施工作业,而实际上不会发生,因而为了减少繁琐计算不考虑活荷载的不利分布,均按满荷载考虑。
其跨内最大弯矩由两部分组成,一个是均布荷载下的最大弯矩,一个是集中力下最大弯矩,最大剪力亦同,查附表3《讲义》32页、33页,得弯矩系数分别为0.08和0.175;剪力系数分别为0.6和0.65,故:
Mmax=0.08×4.7×3.62+0.175×29.7×3.6=23.6(KN.m)
(若把集中力全视为活荷考并考虑活荷载的不利分布,查表其系数为0.213 则Mmax=27.7KN.m)
Vmax=0.6ql+0.65RA=0.6×4.7×3.6+0.65×29.7=29.46(KN)
抗弯、抗剪计算:
α=23.6×106/14.3×750×4652 =0.0102
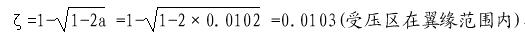
AS=0.0103×14.3×750×465/360 =143(mm2)
实配 2Φ14 As=307>143 满足要求
(按最大M=27.7 KN.m验算显然也满足要求)
与前文已进行的抗剪验算比较,梁的的斜截面抗剪能力足够,验算从略。
续前:
4、《讲义》第7页“二当横杆置于纵杆之下时”
计算简图: 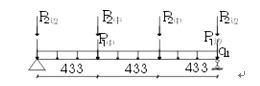
荷载计算“q1(自重)=46.1N/m (已含分项系数,前文已计算)
P2中=施工荷载通过纵杆传来
=3000N/m2×0.43m×1.5m×1.4=1806N
P1中=纵向杆传来其自重及脚手板重
=38.4N/m×1.5×1.2+350N/m2×0.43×1.5×1.2
=340N
支座上的集中力不参与内力计算。
在均布荷载下Mmax=(1/8) qL2H=(1/8) ×46.1×1.32=9.74(N.m)
在集中荷载下其最大弯矩,计算如下 首先将(P1中+ P2中)=2146
合为一个集中力,其计算简图为:

由ΣX=0 得XA=0
由ΣMA=0 得 yB=[(2/3 )LHP+(1/3) LHP]/LH =P
由Σy=0 得yA=P
P从A点到开如向右第一个1/3 段的弯矩方程为:
Mx=Px 到集中力作用处 M=1/3 PLH
在中间的1/3 段,实际上均为1/3 PL
最大弯矩为Mmax2=1/3 PLH=1/3 (P1中+ P2中)LH
=13/ ×1.32×2146=930N.m
Mmax= Mmax1+ Mmax2=930+9.74=940(N.m)
注意:在集中力作用下简支梁的支座反力及内力(弯矩、剪力)会因集中力大小、集中力个数、集中力作用位置的不同而不同,如遇这种情况我必须通过平衡方程求解,为方便各位今后计算,下面是笔者推导的几种集中力下最大弯矩、最大剪力的求解公式:
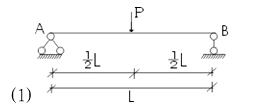 Mmax=1/4 PL RA= RB=1/2 P Vmax=1/2 P Mmax=1/4 PL RA= RB=1/2 P Vmax=1/2 P
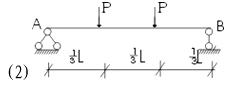 Mmax=1/3 PL RA= RB=P Vmax=P Mmax=1/3 PL RA= RB=P Vmax=P
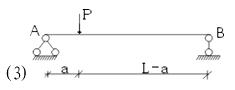 Mmax= Pa(L-a)/L =Pa(1-a/L ) Mmax= Pa(L-a)/L =Pa(1-a/L )
Vmax=(L-a)P/L =P-(a/L)P = P(1-a/L )
RA=(L-a/L) P RB=Pa/L
待续 2010年8月19日
|