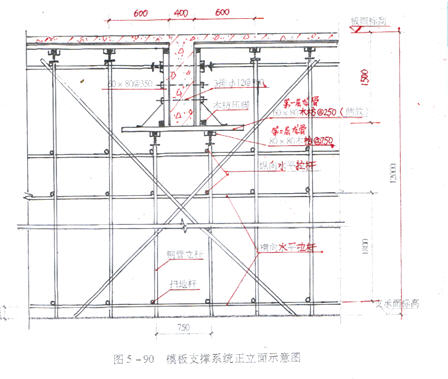
第一层龙骨计算简图
（注：原讲稿引进了c/L =γ的计算参数，因我们一般没有相关计算手册，故此处不采用此法，而用平衡方程直接求解）
a) 梁传荷载： q=梁底面荷载×第一层龙骨间距
=梁底线荷载÷梁宽×第一层龙骨间距
= q1÷0.4×0.25=20.6÷0.4×0.25=12.88 KN/m
=12.88 N/mm
b) 板传荷载：
验算桡度时q’= q2×龙骨间距÷梁宽=16.23×250÷400
=10.14 N/mm
P=通过木枋肋传来板部荷载
=[1.2×(混凝土面荷+模板面荷)+1.4×施工面荷]×0.6/2 ×0.25
=[1.2×(0.15×25+0.3)+1.4×2.5]×0.6/2 ×0.25=0.63KN
(※ 0.62 ×0.25即为每根木枋肋承担荷载之面积)
c) 第一层龙骨内力计算（见下图）：
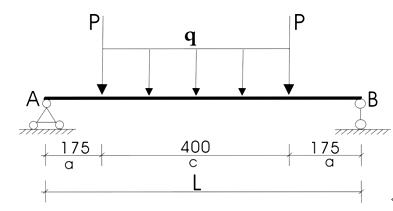
由Σx=0 显然xA=0
由ΣMA=0: yB=[ P×0.175+p×0.575+q×0.4×(0.175+0.4/2 )]/0.75
=(0.75×0.63+12.88×0.4×0.375)/0.75
=(0.473+1.932)/0.75 =3.2(KN)
由Σy=0 得 yA=0.4×q+2P-3.2==3.2(KN)
由于荷载对称,故最大弯矩显然发生在跨中
Mmax=M中=yA×0.75/2 -q/2 ×0.22-P×0.2
=3.2×0.75/2 -12.88×0.22/2 -0.63×0.2
=0.8164≈0.82 KN?m
Vmax=3.2 KN(与支座反力相等)
对于结构力学熟练者来说求最大弯矩，还有更简捷的方法，即
Mmax=yA×0.175+(1/8 q)×0.42
=3.2×0.175+1/8 ×12.88×0.16
=0.817≈0.82 (KN.m)
其弯矩图应为
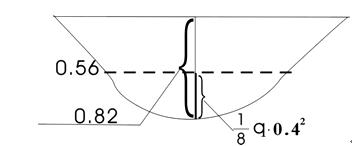
d) 强度验算:
σ= Mmax/w=820000/64000=12.8(N/mm2)
＜fm=13.N/mm2 满足要求
τ=3Vmax/2bh=(3×3.2×1000)÷(2×60×80)
=1.0 N/mm2 ＜fv=1.4N/mm2 满足要求
e) 桡度验算
Vq=q’c(8L3-4c2L+c3)/384EI
=10.14×400(8×7503-4×4002×750+4003)÷(384×900×2560000)
=1.2×1013÷8.85×1012=1.36(mm)
Vp=PaL2[3-4(a/L )2]/(24EI)
=（0.63÷1000）×175×7503[3-4×(175/750 )2]÷(24×9000×2560000)
=4.65×1013×2.78÷(24×9000×2560000)
=1.29×1011÷5.53×1011=0.23mm
V=Vq+Vp=1.59＜L/250 =3 满足要求
协会概况 
学习与讨论
协会简介
协会章程