详解《建筑施工安全专项方案编制讲义》中有关力学计算

一、关于平面平衡力系：
    1、在平面平衡力系中所有X方向力的代数和等于0（向右为正，向左为负）
即：Σx=0
    2、在平面平衡力系中所有Y方向力的代数和等于零（向上为正，向下为负）
即：Σy=0
    3、在平面平衡力系中所有力对任意点O的力矩之代数和为零（顺时针转为正，逆时针转为负）即：ΣM0=0
大部分情况下一个力的方向不会正好平行于x轴或y轴，但我们可把它分解成两个方向的力。
二、简支梁、悬臂梁
    1、简支梁
一个刚体如一根杆件在平面内，如果无任何约束，它可以向左右移动，也可以上下移动，又可以转任一点转动，因此我们说它在平面内有三个自由度。
现在我们假设杆件A、B在平面上处于水平，在A点加一连杆，与一大刚体如大地相连如图1 所示 ： 
              
    这样杆件相对于刚体（大地）就不能上下移动了，但仍可左右移动和绕A点转动，因而它还有两个自由度（我增加一个连杆就是增加了一个约束），它是一个可变体，现在我们又在A点增加一个与原连杆不平行的连杆约束，使它不能左右移动，如图2所示：
        
从而又减少了它一个自由度，A、B杆只能绕A点转动了，它仍是一个可变体。现在再在B点加一连杆与大地相连如图3所示：
                         
这时杆件A、B就稳定了它们自由度为0成了不可变体，这就是我们常说的简支梁，（有自由度的可变体是不能作结构的）。
在工程中，一块预制板两端搁置于墙上，我们可以视为简支梁，在两砖柱上浇筑一根钢简混凝梁，我们也可以视为简支梁，有时这种梁向一端或两端伸出一段，则构成了简支伸臂

梁。
    2、悬臂梁  工程中有的梁一端嵌固于墙体中，由于嵌固作用它即不能上下移动，也不能左右移动，也不能转动，这就是我们所说的悬臂梁，悬臂梁、简支梁是最简单的静定结构。
    3、连续梁 在几个桥墩上连续浇筑一座桥这座桥我们可以视为连续梁。
根据连续梁的跨数多少可分为：二跨、三跨、四跨……….n跨连续梁。
根据连续梁的跨度相等与不相等又分为等跨和不等跨连续梁。显然连续梁是有多余约束的超静定结构。
我们可以用平面力系的平稳方程：
                     Σx=0      Σy=0    ΣM0=0
求解在外力作用下静定结构的受力情况和支座反力，对于超静定结构就不能简单地用平衡方程去求解了。
三、详解有关计算
    1、“讲义”第十八页：
                
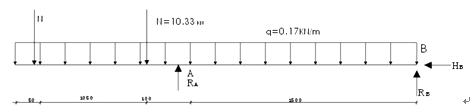
① 解除支座约束，用支座反力代替约束，A点只一连杆约束只有一个垂直反力，B点有两根不平行的相交连杆（铰）有水平和垂直两个方向的反力。
               
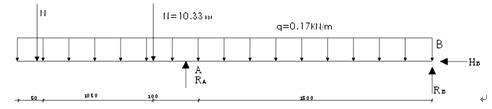
设A点反力为R_A（亦可设为YA）B点反力为RB（YB）HB（XB） 
由ΣMA=0  得：12 ×0.17×1.52-RB×1.5+HB×0
            -12 ×0.17×1.22-10.33×1.15-10.33×0.1=0
  R_B=12 ×0.17×1.22+10.33×1.15+10.33×0.1-12 ×0.17×1.521.5
 =-8.56 KN(拉)    与假设的方向相反
由Σy=0  得：（向上的垂直为正，向下的为负）
R_A+R_B-2N-2.7×q=0
A_A=2N+2.7×0.17-R_B=2×10.33+2.7×0.17-(-8.56)
   =29.7  (KN)  (原计算与更正后计算均有错)
  由Σx=0  得H_B=0
   Mmax=1.15N+0.1N+(1/2) q×1.2²=13(KN.m)
   Vmax=20.9 KN

                                  待续  2010年8月13日